November 2nd, 2022
An Attempt at Evolutionary Melody Generation
A demo of the app
This is a webapp I made in December 2020 and am just now getting to writing about. You can view it here.
The idea is to selectively breed melodies with a human in the loop as the fitness test.
Algorithm
More accurately, we breed music generators, or “organisms” as I will refer to them here. Each organism has a set of equations that determine how it generates melodies—this would be the metaphorical genome.
The algorithms I used to both generate organisms’ equations and the subsequent melodies are designed by myself and completely arbitrary.
Generating Melodies
Each organism has two member equations—probability distributions for rhythm/note duration and for pitch. These functions take a pitch/duration as an input, and yield the relative probability of it being output by the organism. Each equation is composed of constants, trigonometric and algebraic operators, variables for the durations and pitches of the melody’s last three notes, and, of course, the input variable \(x\).
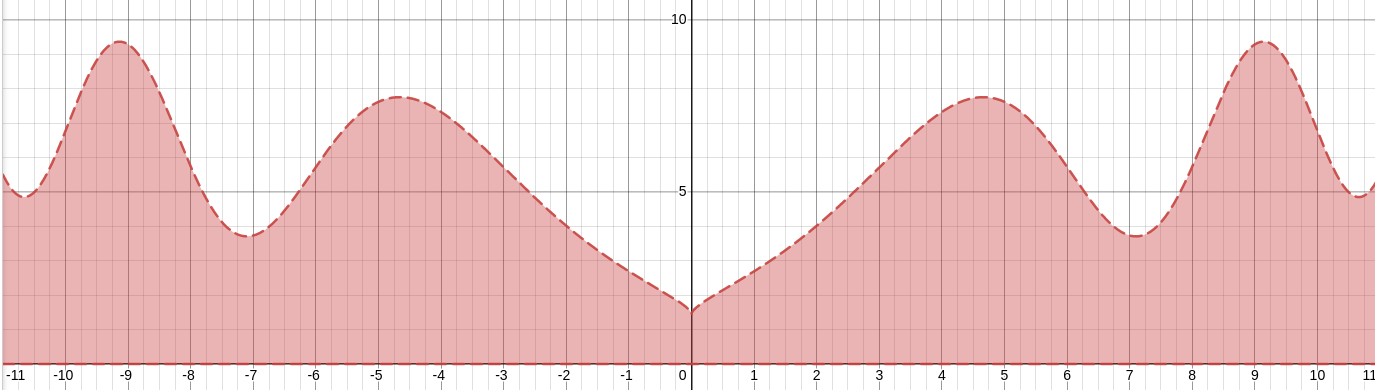
A graph of a probability distribution for pitch with the equation \(5cos^2(\dfrac{x^2}{20}-1) + x^{\frac{2}{3}}\)
For example, in the graph above, the peaks around \(x = \pm 9\) tell us that a note nine scale degrees above or below the center note is most likely to be output by this organism, and the dip at \(x = 0\) that the center note itself is least.
The organisms generate melodies note by note, randomly picking pitch and duration with these distributions.
Populating The Bracket
First generation organisms are initialized with randomly generated equations of varying length.
After that, each organism generates two melodies that are put against each other in a randomly seeded bracket. The next generation is created from the winning N (four in my current implementation) through permutation and mutation.
Permutation populates the bracket with every possible combination of winning equations, each organism contributing half its “genome.”
Mutation does one of four things:
- Replaces a random operator/operand in an equation with another
- Scales a constant by a random factor
- Deletes a random operator, and operand(s) if the operator is not unary
- Inserts a random operator (and operand(s))
Each generation comprises all permutations of winning genomes, N mutants (five, currently), the previous generation’s unaltered winners, and N=3 random new organisms.
Implementation
A webapp lets multiple users vote on brackets at the same (or not same) time. This made sense for this project since multiple users means faster generation cycles and less bias.
API
The API is written in Python with Flask, hosted on Heroku alongside a PostgreSQL database for bracket data, and has two endpoints: one to request a pair to vote on, and one to cast a vote.
The first takes GET requests with no arguments and yields two base64-encoded MIDI melodies and their respective identifiers, if any are available.
The second takes POST requests with arguments for the pair and loser’s identifiers, and eliminates the loser from the bracket. If the pair was the last of a bracket tier, new pairs are generated for the next tier. If the pair was the last of the entire bracket, a new bracket is generated from the top organisms as described above.
UI
A still of the UI
The UI is written in plain HTML, CSS, and JavaScript. It is minimalistically designed with graphics I made myself. A random background color is selected and a pair fetched on page load. There are buttons to hear and select each song, cast your vote, and that’s about it.
You can view the source for the UI here and a demo here.
Results
The app was a success in that it functions without error and correctly implements the algorithms described above. The algorithm itself, however, is naive—so far, the melodies do not appear to be growing any more pleasant, nor my methods of genetic recombination to yield organisms similar to their two parents for that matter. I am interested to see what would come of this idea if it used something like Magenta’s MusicVAE to represent melodies in a latent space, where operations performed on melodies have more intuitive results.