October 22nd, 2024
Hunting Words for Fun and No Profit

The app in action
I like Word Hunt. I don’t even have an iPhone (I use a Pixel running GrapheneOS), but I borrow them so often to play that my “obsession” with the game has become a bit.
I created this web app at the height of this in summer of 2024. I was initially motivated by questions about optimal play and score distributions but ended up building a solver that finds all words and on a board and the maximum achievable score.
You can try it out here. You can also view the source code on GitHub.
The Game

A screenshot of a Word Hunt board
For the uninitiated, Word Hunt is a lot like Boggle. The goal of the game is to find as many words as you can on a board like above in the time allotted. You construct words by connecting adjacent letters on the grid (e.g., “laser” would be a word on this board, though I leave finding it as an exercise for the reader). Diagonal moves are allowed and each tile can only be used once in a word. Longer words give you more points.
Reading Boards

A webcam image before and after preprocessing and board identification. All squares found are boxed in red. Those identified as tiles, in green.
Since games are timed at 80 seconds, having users type in each letter of their board was not an option. I opted instead to use OpenCV to read in the board from an image.
The logic for this was relatively simple:
- First, do standard pre-processing (convert the image to grayscale and binarize)
- Use OpenCV to find contours (edges of shapes)
- Approximate each contour as a quadrilateral
- Compare contour positions and dimensions to look for a large square with a 4x4 grid of smaller squares inside of it. If that’s found:
- Split the image into its 16 tiles
- Iterate through them left to right, top to bottom, and use template matching* to correspond each to a letter.
If all tiles are found and each matches a character, the result is a 2D array of characters representing the game board.
*I tried a few other methods including tesseract and EasyOCR, but this worked the best. This meant that I needed 26 reference images to cover all possible letters that could appear on the board. Most of these were available online from random screenshots and videos, but I did have to play ~20 games on my girlfriend’s phone to find a board with a ‘Z’ I could screenshot.
Hunting Words
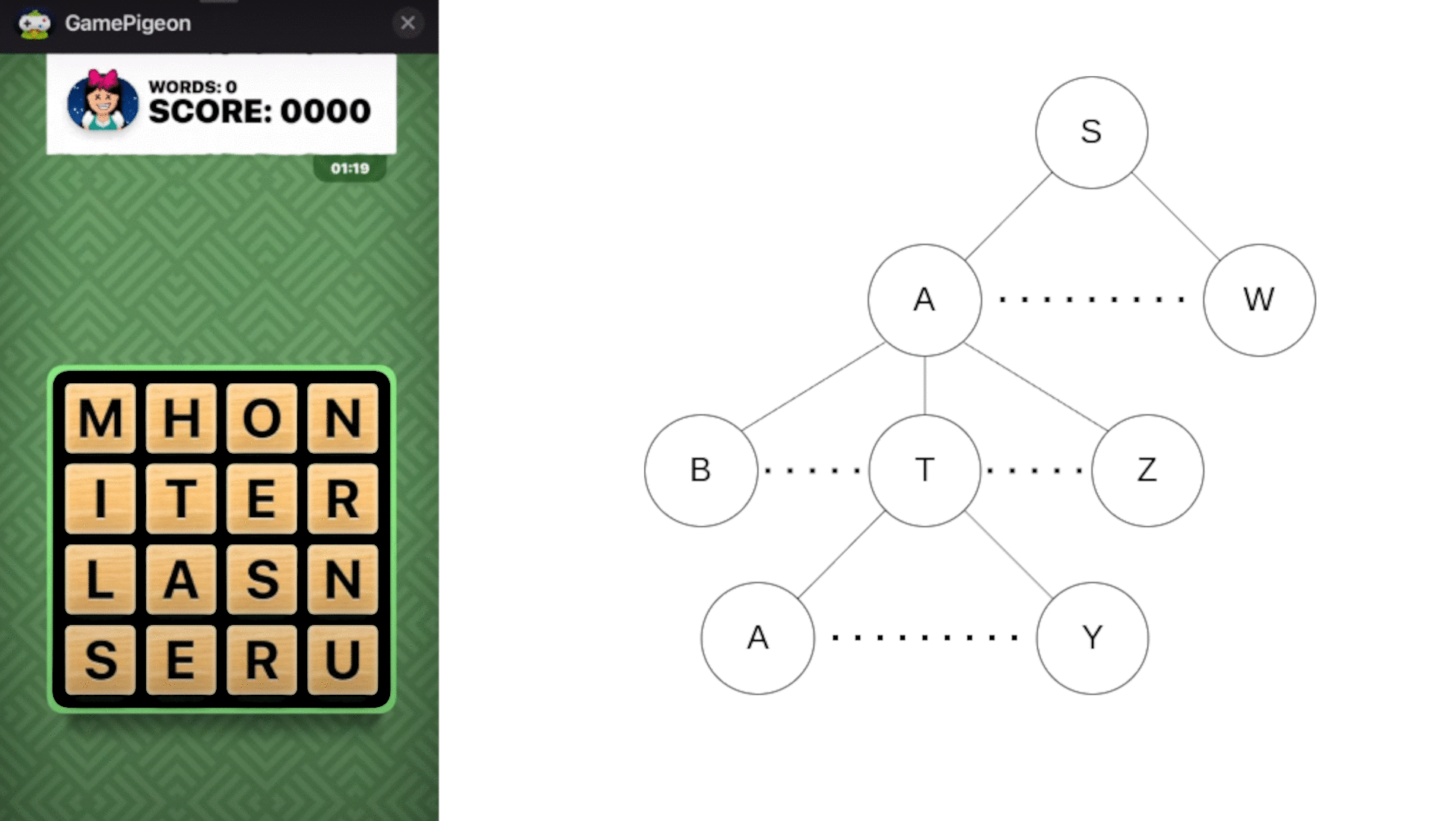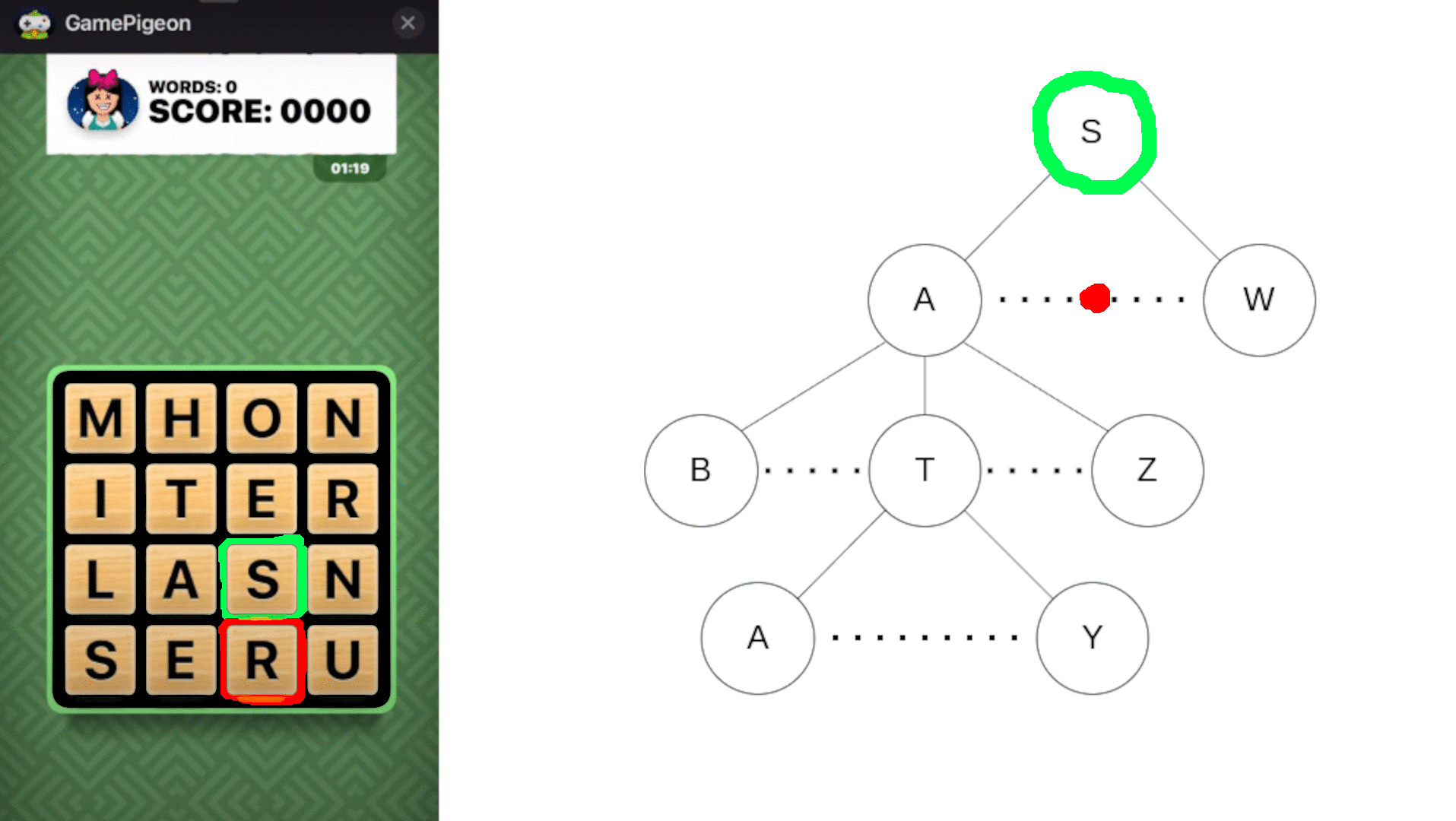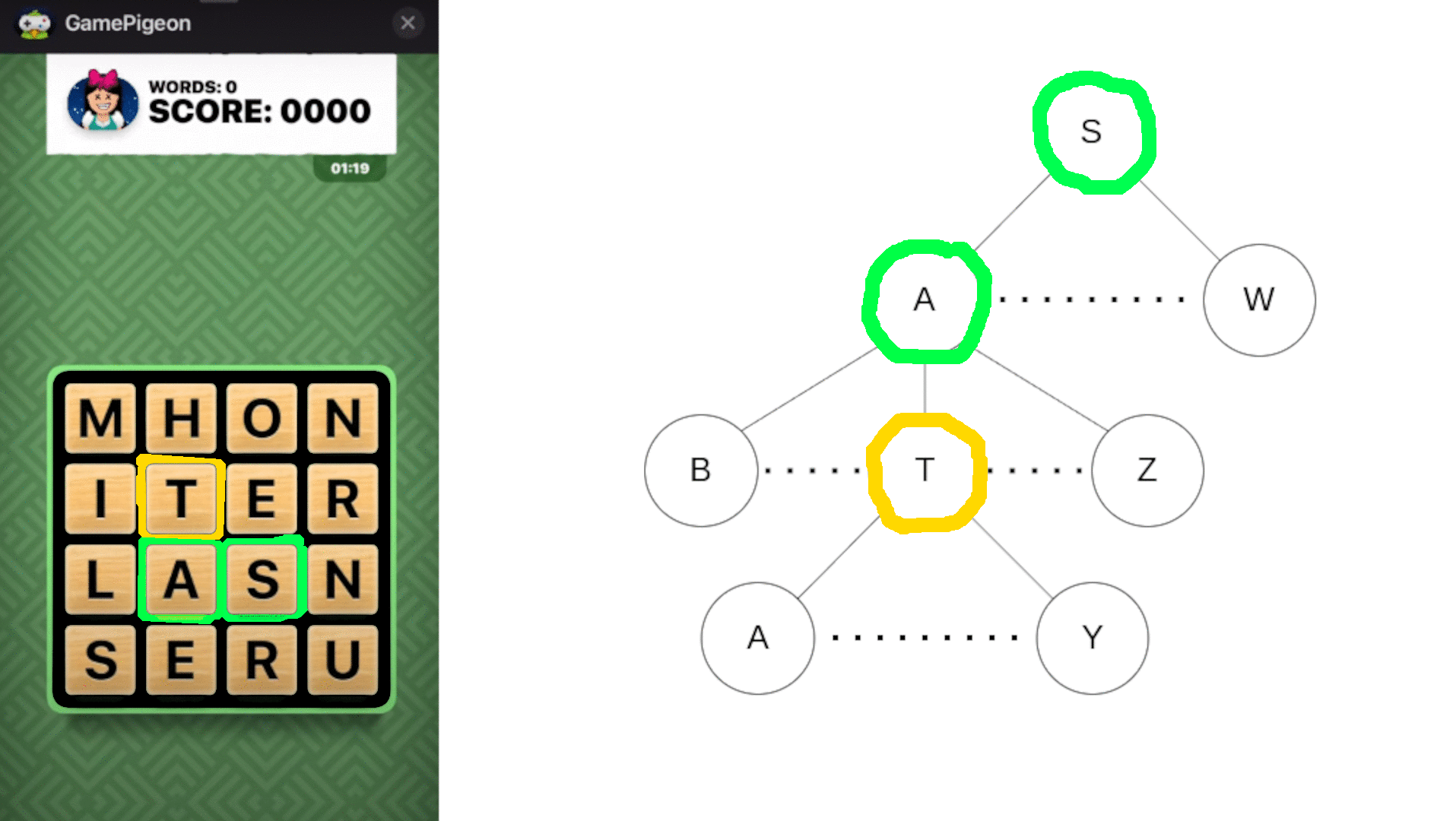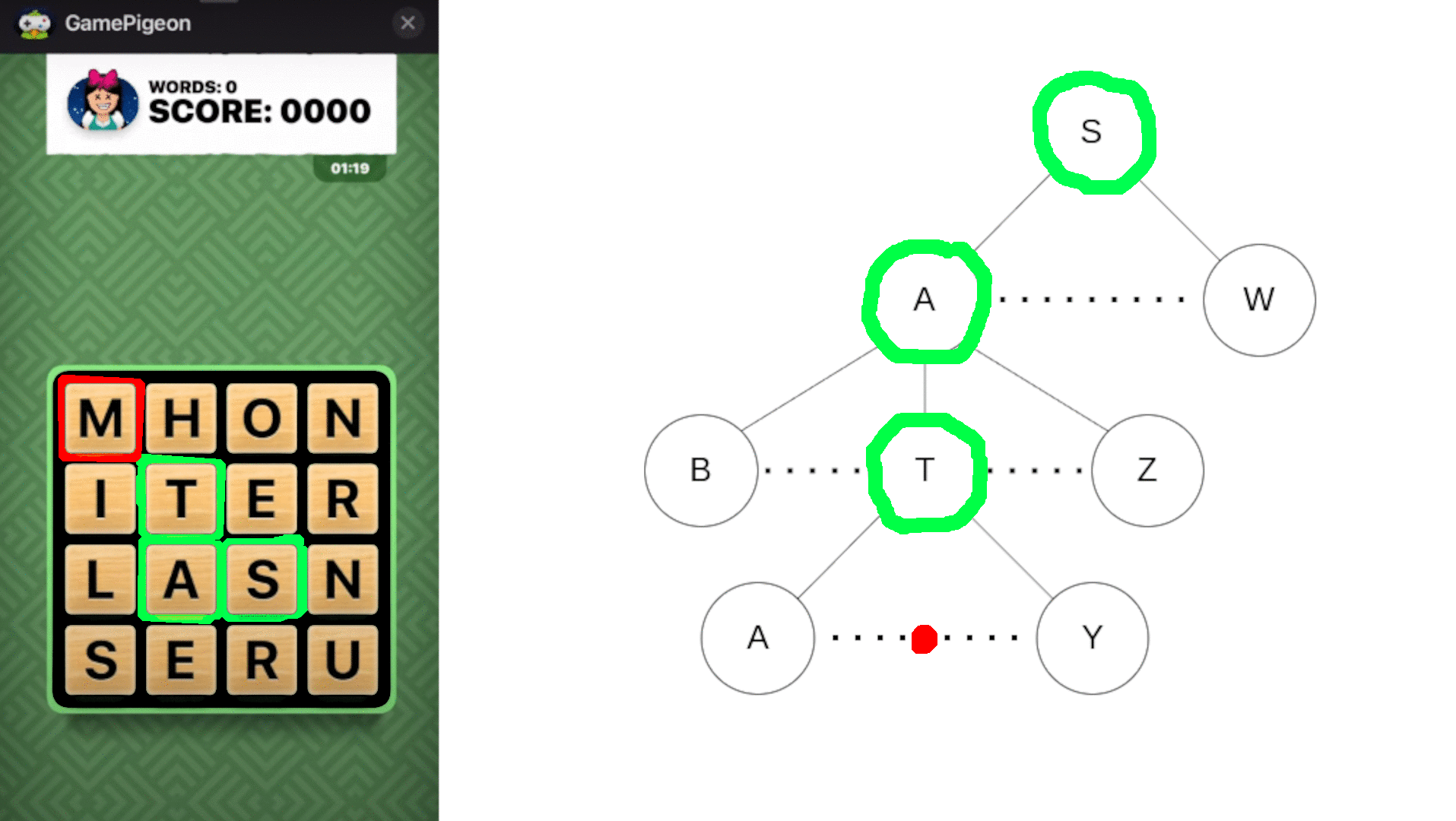
An animation showing early stopping with a trie. The paths branching from the red-boxed R and M are skipped because no English words begin with 'SR' or 'SATM'.
Solving the board by brute force (trying all possible letter combinations) is greatly suboptimal and not likely to run quick enough on more limited hardware. Instead, I used a trie, which stores an entire dictionary as a tree where branches are possible next characters and nodes indicate whether a string is a valid prefix or word. Importantly, a node only has branches for next characters that could lead to a real English word, not always for all 26 letters. Resultant dead ends allow the program to stop exploring paths that can’t lead to valid words. For example, since no English word starts with ‘wx’, the program can immediately skip further checks once it reaches that combination.
In pseudo-code, the algorithm looks like this:
- Initialize an empty list of words
- For each tile on the board:
- Initialize an empty word string
- Append the current tile’s letter to the word string
- Check if the current string is a valid prefix according to the trie
- If it is not, end this branch
- Check if the current string is a valid word according to the trie
- If it is, add it to the word list
- For each possible next move:
- Branch to that tile
- Go back to step 2 and repeat
Though using a trie doesn’t technically improve the worst case time complexity, the early stopping significantly helps the average.
Scoring
To rank words and calculate a board’s maximum score, I needed a function that tells how many points a word is worth. Empirically, I found this to be
with \(n\) being the length of the word. (Words of length 1 and 2 are not valid in this game.)
Web App

A still of the web UI
My initial implementation of this was a Python CLI, but I thought a web app would look nicer and be easier to use. Luckily, OpenCV has a JS library that’s pretty much one-to-one with the Python version, so porting that over was pretty easy. Reimplementing the solve logic was also pretty straightforward, though I did end up implementing the trie from scratch rather than using a library like I did in Python.
The most time consuming part was without a doubt the UI, which I painstakingly styled to match GamePigeon’s as closely as possible.*
*I even drew out the tiled background pattern myself in GIMP. I eventually gave up on recreating it perfectly and went with a simplified version because the original was messing with my head too much.